新公微信公眾號(hào)【新公教育】(cqxgjy)     |        備考QQ群：820473978      |       備考課程：三年協(xié)議無限學(xué)

———————————————————————————————————

2021年省考已成過去，2022年省考已悄然而至，相信同學(xué)們也早早開始備考了。在行測(cè)考試中，經(jīng)常會(huì)考到行程問題，同時(shí)行程問題也讓很多同學(xué)感到頭疼，因?yàn)樗泻芏嘀R(shí)點(diǎn)，而其中一個(gè)就是相遇追及模型下的牛吃草問題。那牛吃草問題和行程問題有什么關(guān)聯(lián)呢，那就一起來學(xué)習(xí)一下吧。

何為牛吃草問題

1.題型展示：英國(guó)著名的物理學(xué)家牛頓曾編過這樣一道題：牧場(chǎng)上有一片青草，每天都生長(zhǎng)得一樣快。這片青草供給10頭牛吃，可以吃22天，或者供給16頭牛吃，可以吃10天，期間一直有草生長(zhǎng)。如果供給25頭牛吃，可以吃多少天?

總結(jié)：牛吃草問題的本質(zhì)描述是有一定的原始量，兩個(gè)未知量對(duì)其進(jìn)行此消彼長(zhǎng)的消耗，所求為消耗時(shí)間或?qū)ο髠€(gè)數(shù)。

2.題型特征：

(1)固定初始量(原有草量)

(2)勻速變化量(草生長(zhǎng)的速度、牛吃草的速度)并影響固定初始量

(3)相似句、排比句

3.公式：

原有草量M=(N±x)×t

注：設(shè)每頭牛每天吃草量為1，草每天生長(zhǎng)量為x，記牛頭數(shù)為N頭，原有草量為M。

例題精講 例1某牧場(chǎng)長(zhǎng)滿牧草，牧草每天均勻生長(zhǎng)，牧場(chǎng)可供100頭牛吃20天，可供150頭牛吃10天，則這片牧場(chǎng)可供250頭牛吃( )天。

A.5 B.6 C.7 D.8

【解析】A。設(shè)每頭牛每天吃1份草，草每天生長(zhǎng)x份，250頭牛t天可以吃完，根據(jù)原有草量相同，則有(100-x)×20=(150-x)×10=(250-x)×t，解得 x=50，t=5，即250頭牛5天可以吃完牧草，選A。

例2某礦井發(fā)生透水事故，且礦井內(nèi)每分鐘涌出的水量相等，救援人員調(diào)來水，如果用兩臺(tái)抽水機(jī)抽水，預(yù)計(jì)40分鐘可抽完;如果用4臺(tái)同樣的抽水機(jī)，16分鐘可抽完。為贏得救援時(shí)間，要在10分鐘內(nèi)抽完礦井內(nèi)的水，那么至少需要抽水機(jī)( )。

A.5臺(tái) B.6臺(tái) C.7臺(tái) D.8臺(tái)

【解析】B。此題中的原有草量實(shí)際為事故發(fā)生后已滲進(jìn)的水量， “牛”即抽水機(jī)，“草”即水，抽水機(jī)在抽水，同時(shí)水在不斷涌入，抽水機(jī)和水同時(shí)對(duì)原來滲進(jìn)的水量進(jìn)行此消彼長(zhǎng)的消耗，且滿足原有草量M=(N±x)×t。設(shè)每臺(tái)抽水機(jī)每分鐘抽水量為1，礦井內(nèi)每分鐘涌出的水量為x，所求為N，則可列方程(2-x)×40=(4-x)×16=(N-x)×10，解得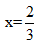N=6。那么10分鐘內(nèi)抽完水，需要6臺(tái)抽水機(jī)，選B。

總結(jié)：若在考試中遇到結(jié)合實(shí)際背景的牛吃草問題，首先通過題型特征進(jìn)行判斷，并找到實(shí)際問題中與“草”和“牛”對(duì)應(yīng)的量再代入公式即可求解。

例3由于天氣逐漸冷起來，牧場(chǎng)上的長(zhǎng)不僅不生長(zhǎng)，反而以固定的速度在減少。已知某塊草地上的草可供20頭牛吃5天，或者可供15頭牛吃6天。照此計(jì)算，可供多少頭牛吃10天?

A.4 B.5 C.6 D.7

【解析】B。牛在吃草，而草也在勻速減少，故為牛吃草中的相遇問題，設(shè)每頭牛每天吃1份草，草每天減少x份，可供N頭牛吃10天，根據(jù)原有草量相同，則有(20+x)×5=(15+x)×6=(N+x)×10，解得 x=10，N=5，選B。

總結(jié)：若兩個(gè)勻速變化的量都使原有草量減少，則為相遇型牛吃草問題，代入基本公式M=(N+x)×t即可求解。

總結(jié)：若為極限思維的牛吃草問題，讓每天草的生長(zhǎng)量=每天牛吃草的量即x=N便可解題。

相信經(jīng)過中公教育的講解，同學(xué)們已經(jīng)了解并掌握了牛吃草問題，在以后做題過程中再遇到牛吃草問題，只需根據(jù)牛吃草問題的特征判斷出題型，再代入公式中即可求解。

新公教育為你提供更多考試資訊和招聘公告可關(guān)注微信公眾號(hào)【新公教育（cqxgjy）】查看！